Mediatoare

În geometria plană, mediatoarea este perpendiculara dusă prin mijlocul unui segment. Mediatoarea poate fi definită și ca fiind locul geometric al punctelor egal depărtate de extremitățile segmentului.
Proprietăți
1. Cele trei mediatoare ale laturilor unui triunghi sunt concurente într-un punct care este centrul cercului circumscris triunghiului.
- Demonstrație. Fie O – punctul de intersecție al mediatoarelor segmentelor AB și BC. Din definiția mediatoarei, rezultă că ceea ce înseamnă că O aparține mediatoarei segmentului AC. [1]
2. Proprietate: Un punct aparține mediatoarei unui segment dacă și numai dacă are distanțe egale față de extremitățile segmentului.
-
 Centrul cercului circumscris al unui triunghi ascuțitunghic se află în interiorul triunghiului.
Centrul cercului circumscris al unui triunghi ascuțitunghic se află în interiorul triunghiului. -
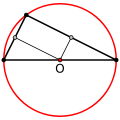 Centrul cercului circumscris al unui triunghi dreptunghic coincide cu mijlocul ipotenuzei.
Centrul cercului circumscris al unui triunghi dreptunghic coincide cu mijlocul ipotenuzei. -
 Centrul cercului circumscris al unui triunghi obtuzunghic se află în exteriorul triunghiului.
Centrul cercului circumscris al unui triunghi obtuzunghic se află în exteriorul triunghiului.
3. Diametrul cercului circumscris este dat de formula:
unde a, b și c sunt lungimile laturilor unui triunghi oarecare, iar p este perimetrul acestuia.
Note
- ^ Augustin Coța, Mariana Răduțiu, Marta Rado, Florica Vornicescu, Geometrie și trigonometrie, 1992, Ministerul Învățământului și Științei, Editura Didactică și Pedagogică, R.A., București, ISBN 973-30-1859-7
Vezi și
- Bisectoare
- Mediană
- Înălțime (geometrie)
 | Acest articol legat de matematică este deocamdată un ciot. Poți ajuta Wikipedia prin completarea lui. |
















